MATLAB中矢量场图的绘制 (quiver/quiver3/dfield/pplane)

发表于 分类于 ， 阅读次数： Disqus： 本文字数： 614 阅读时长 ≈ 2 分钟

quiver函数

一般用于绘制二维矢量场图，函数调用方法如下：

1
quiver(x,y,u,v)

该函数展示了点(x,y)对应的的矢量(u,v)。其中，x的长度要求等于u、v的列数，y的长度要求等于u、v的行数。在绘制图像的过程中，通常用meshgrid来生成所需的网格采样点。

下面举几个例子：

例1：一个最简单的例子，该二维矢量场图中的矢量皆从(0,0)出发，分别指向(1,0) 、(-1,0) 、(0,1) 、(0,-1)。

1
2
3
4
5
x=[0 0 0 0];
y=x;
u=[1 -1 0 0];
v=[0 0 1 -1];
quiver(x,y,u,v)

画出下图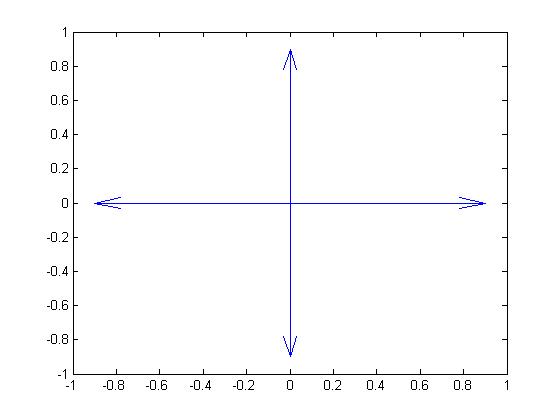

但我们发现箭头并没有完全指到(1,0) 、(-1,0) 、(0,1) 、(0,-1) 。如果需要箭头完全指到(1,0) 、(-1,0) 、(0,1) 、(0,-1)，我们需要改变scale参数，将其设为1。参考方法如下：

1
quiver(x,y,u,v,1)

　画出图像如下 ：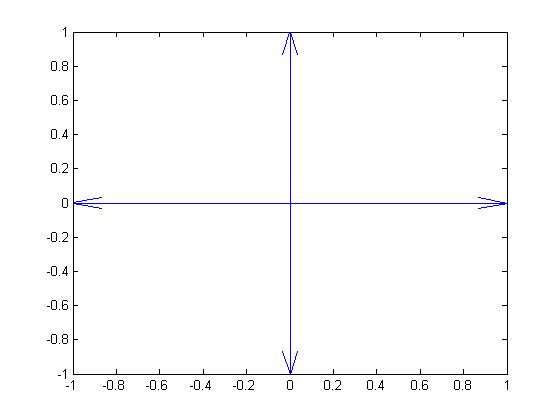

当然，也可以改变颜色。改变颜色可以参考LineSpec的设置，参考代码如下：

1
>> quiver(x,y,u,v,'-r')  %这里将图像设置为红色

　画出图像如下：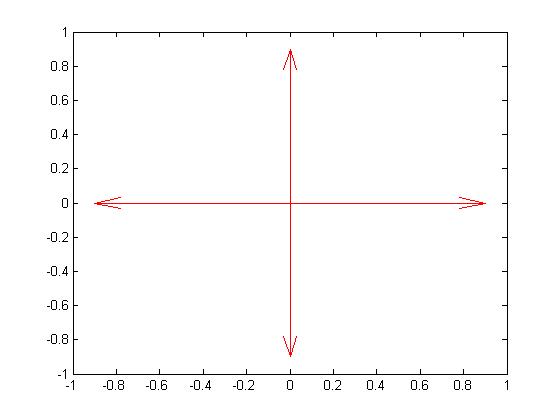

例2：(参考MathWorks)：已知$$u=y\ cos(x), v = y\ sin(x)$$

1
2
3
4
[x,y] = meshgrid(0:0.2:2,0:0.2:2);  %生成所需的网格采样点 x与y在0到2区间 每隔0.2取一个点
u = cos(x).*y;
v = sin(x).*y;
quiver(x,y,u,v) %绘制二维矢量场图

画出下图: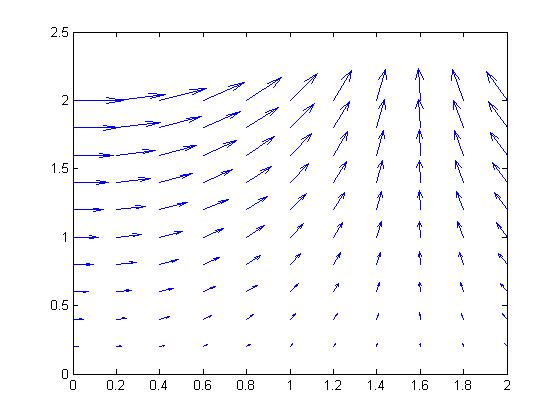

quiver3函数

用法与quiver类似，用于三维矢量场图的绘制。

例3: (参考MathWorks)绘制$z=y^2-x^2$的三维矢量场图。

1
2
3
4
>> [x,y]=meshgrid(-3:.5:3,-3:.5:3); %生成所需的网格采样点 x与y在-3到3范围内 每隔0.5取一个点
>> z=y.^2-x.^2;
>> [u,v,w]=surfnorm(z); %取三维曲面的法线
>> quiver3(z,u,v,w)  %绘制三维矢量场图

画出下图：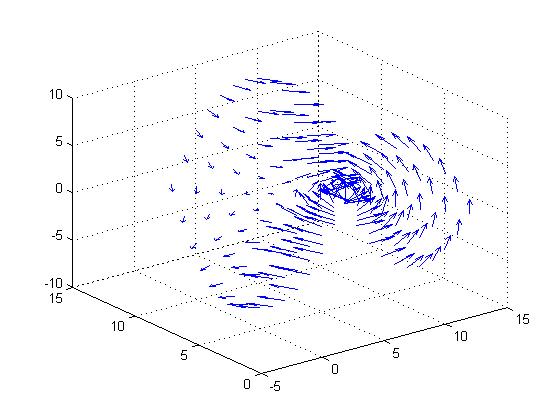

dfield与pplane(多应用于常微分方程)

dfield与pplane的原作者是Rice University的John C. Polking，用于解决涉及常微分方程的问题，比较方便，这里可以下载dfield与pplane的.m文件

在MATLAB中调用dfield，呈现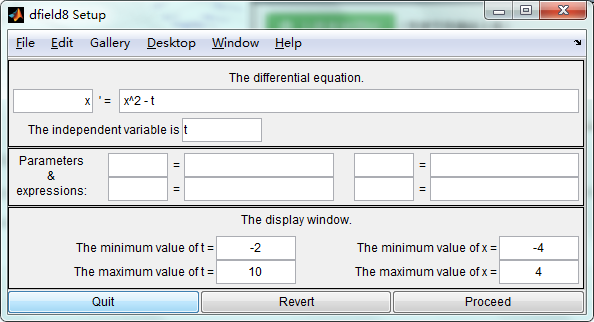

如果我们要绘制常微分方程$x’=x^2-t$ 对应的矢量场图，我们可以输入对应的公式与参数值。在这里，上图中默认的常微分方程对应矢量场图：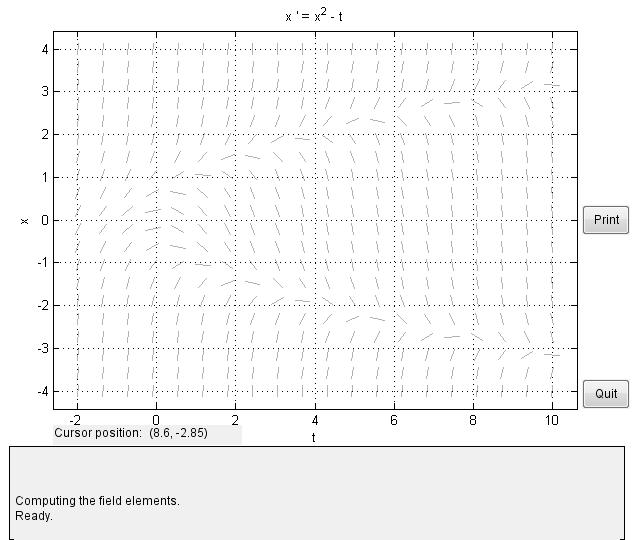

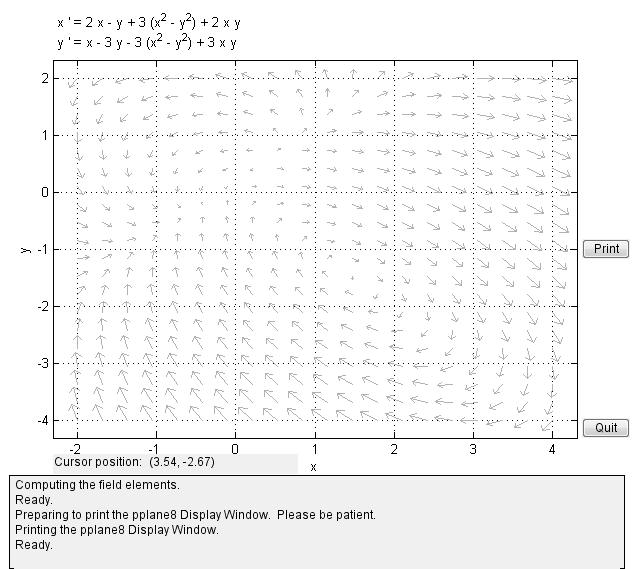
在MATLAB中调用pplane，呈现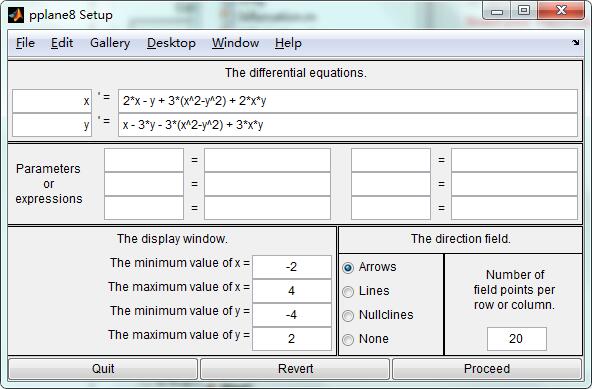
以默认的微分方程为例，可以绘制矢量场图：