【算法分析】如何理解快慢指针？判断linked list中是否有环、找到环的起始节点位置。以Leetcode 141. Linked List Cycle, 142. Linked List Cycle II 为例 | Python实现

发表于 分类于 ， 阅读次数： Disqus： 本文字数： 1.4k 阅读时长 ≈ 5 分钟

引入

快慢指针经常用于链表(linked list)中环(Cycle)相关的问题。LeetCode中对应题目分别是：

简介

  • 快指针(fast pointer)和慢指针(slow pointer)都从链表的head出发。
  • 慢指针每次移动一格，而快指针每次移动两格。
  • 如果快慢指针能相遇，则证明链表中有环；否则如果走到头了依然没有相遇，则没有环。

快慢指针的具体代码(C++, Python, Java版本)可以参考这个链接。

问题详解 - 为什么如果有环，则快慢指针必定会相遇？

如果链表里有环，那么环的初始状态大概是像下图这样的：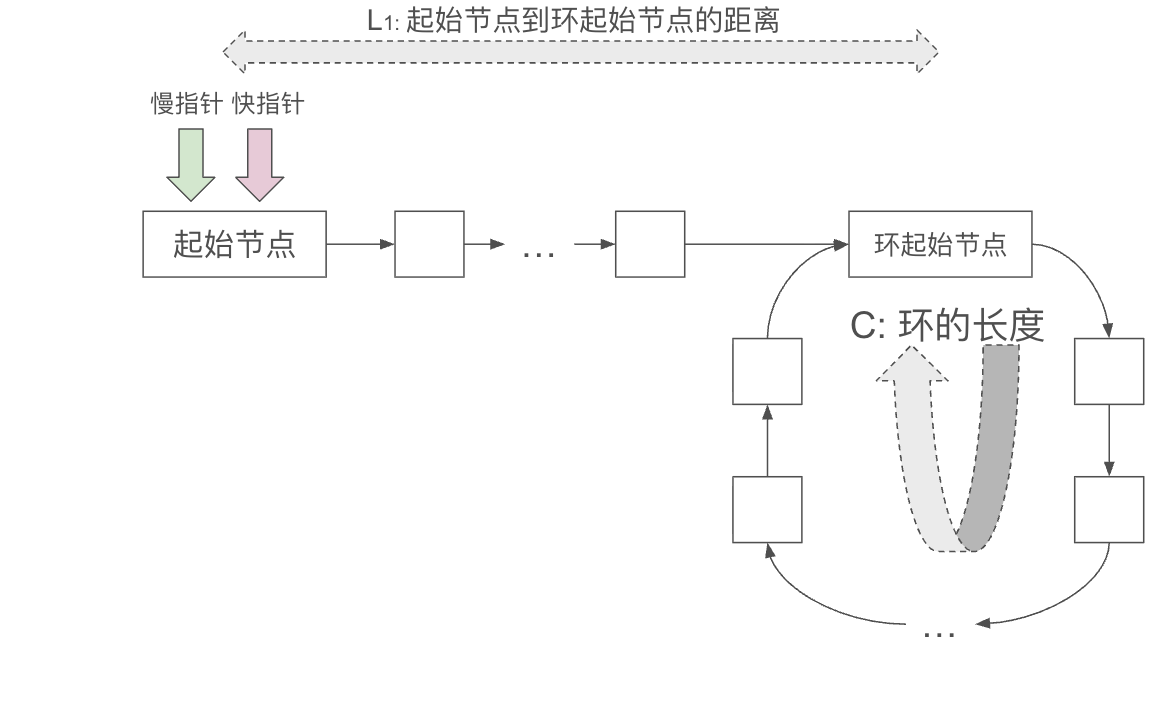

从数学的角度来分析，我们假设以下三个变量：

  • $L_1$: 起始节点(head node)到环起始节点(entry node)的距离。当然，如果起始节点和环起始节点是同一个节点，那么这个距离也可能为0。
  • $C$: 从环起始节点出发，绕一圈后再回到起始节点所需要走的距离，这里有环的话，就必有 $C\gt 0$。
  • $x$: 慢指针移动的距离。假设我们的慢指针移动了 $x$ 步，那么快指针就移动了 $2x$ 步。

已知对于一个给定的链表，$C$ 和 $L_1$ 都是固定值，不会产生改变。而慢指针每走一步，$x$都会上升。那也就是说，随着 $x$ 上升，必定会有一个时刻存在一个整数 $w$，使得 $x=w\cdot C$。那么也就是说一定存在一个 $x$ 使得以下这个式子成立：
$$x \equiv 0 \pmod{C}$$
那么以下这个式子也成立：
$$2x \equiv 0 \pmod{C}$$
可以得出：
$$2x \equiv x \pmod{C}$$
再在两边都减去$L_1$，得出：
$$2x-L_1 \equiv x-L_1 \pmod{C}$$
$2x-L_1 \pmod{C}$ 是此时快指针在环里距离环起始节点的距离，$x-L_1 \pmod{C}$ 是此时慢指针在环里距离环起始节点的距离，而他们是一样的，说明此时快指针和慢指针是在同一个节点上的。也就是说，到这里我们从数学的角度证明了：只要有环，快慢指针一定会相遇。而且相遇的时候，慢指针走过的距离 $x$ 一定是环长 $C$ 的倍数。

问题详解 - 如何找到环的起始节点？

刚才我们已经证明了，假设链表有环，那么当快慢指针走了一阵子后，一定会在环里某一个地方相遇。并且相遇的时候，慢指针走过的距离 $x$ 一定是环长 $C$ 的倍数。

我们想要找到环的起始节点，其实本质上就是想知道，$L_1$ 到底是多少。

参考以下图片，假设我们的快慢指针在环里某个地方相遇。

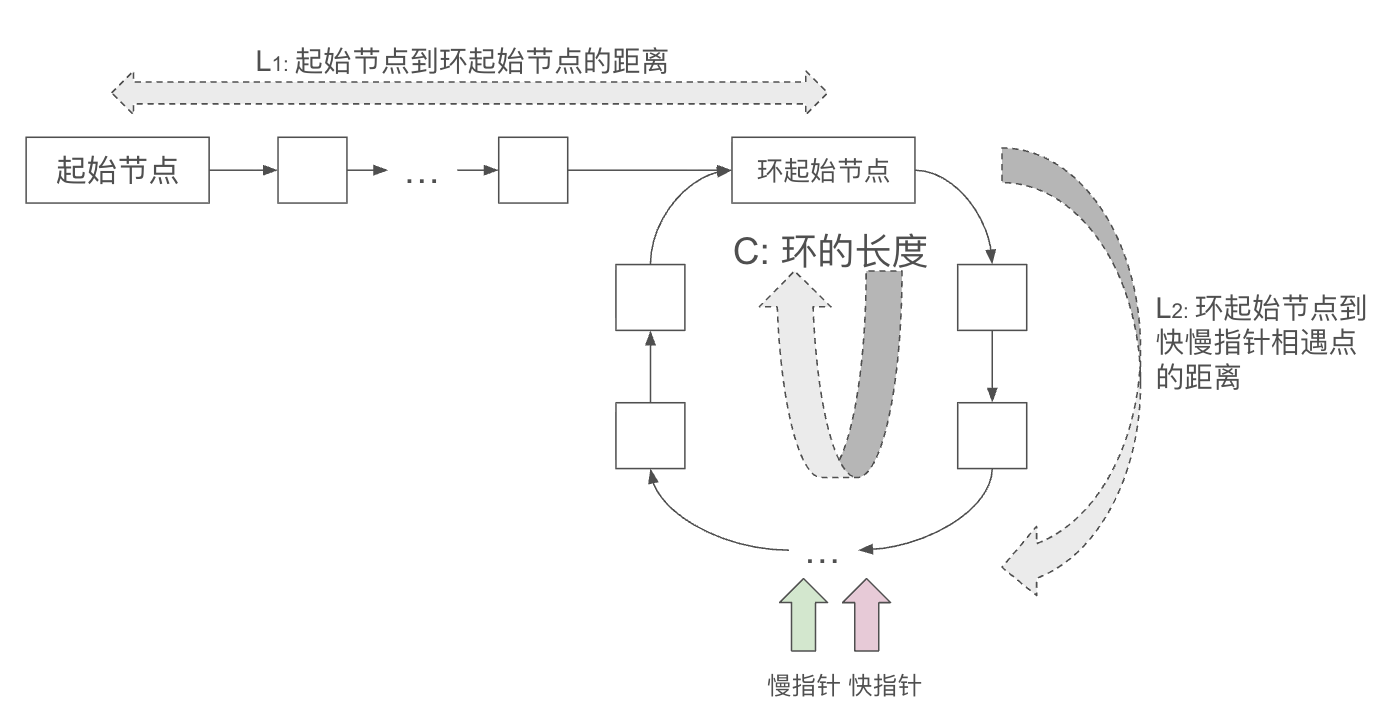
我们现在定义以下变量：

  • $x$: 慢指针和快指针相遇的时候，慢指针走了的距离。
  • 注意到，因为快指针走了的距离总是慢指针走了的距离的两倍，因此 $2x$ 是慢指针和快指针相遇的时候，快指针走了的距离。

我们再补充一个变量:

  • $L_2$: 环起始节点(entry node)到快慢指针相遇节点的距离。

当快慢指针相遇的时候，一定有 $x=L_1+L_2+n C$，这里 $n$ 是指慢指针在环内走过的完整圈数。因此可以得出：
$$L_1+L_2=x-n C$$
已知相遇的时候有
$$x \equiv 0 \pmod{C}$$
而且以下式子一定成立
$$nC \equiv 0 \pmod{C}$$
因此$$x-nC \equiv 0 \pmod{C}$$
那么$$L_1+L_2 \equiv 0 \pmod{C}$$所以$$L_1 \equiv -L_2 \pmod{C}$$ 也有 $$L_1 \equiv C-L_2 \pmod{C}$$
而右边的 $C-L_2$ 也正是慢指针在环内想要再次到达环起始节点所需要走的距离。
因此，我们如果再用两个指针分别从起始节点(head)和刚才快慢指针的相遇点出发，以同样的速度移动，那么他们在某一个时间一定会在环起始节点(entry node)相遇。
这里我们可能会问，为什么我们能确定这两个指针第一次相遇的点一定是环起始节点(entry node)而不是别的呢？假设这个新的从起始节点(head)出发的指针走了 $t$ 步，当 $t\lt L_1$ 时，他们必不可能相遇，因为这个新的从起始节点(head)出发的指针还不在环内。而当 $t=L_1$ 时，我们刚才证明了他们一定会相遇。

LeetCode对应问题及其代码实现

判断Linked List中是否有环 (141. Linked List Cycle)

LeetCode 141. Linked List Cycle - 判断Linked List中是否有环

  • 时间复杂度O(n)
  • 空间复杂度O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def hasCycle(self, head):
        """
        :type head: ListNode
        :rtype: bool
        """
        if head is None:
            return False
        slow = head
        fast = head
        while(fast.next and fast.next.next):
            slow = slow.next
            fast = fast.next.next
            if slow == fast:
                return True
        return False

找到环的起始节点(entry node)位置 (142. Linked List Cycle II)

142. Linked List Cycle II - 找到环的起始节点（Entry Node）位置

  • 时间复杂度O(n)
  • 空间复杂度O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution(object):
    def detectCycle(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        if head is None:
            return None
        slow, fast, new_node = head, head, head
        while(fast.next and fast.next.next):
            slow = slow.next
            fast = fast.next.next
            if slow == fast:
                while slow != new_node:
                    new_node = new_node.next
                    slow = slow.next
                return new_node      
        return None